


Thus, we can say, integers are numbers that can be positive, negative or zero, but cannot be a fraction. Similar to whole numbers, integers also does not include the fractional part. If the car moves along the $-$ direction and the time the video is played is positive, i.e. In Mathematics, integers are the collection of whole numbers and negative numbers. Therefore the following holds: $$\rm positive\times positive=positive.$$ the video is played normally, then you'll see that the car moves along the $+$ direction and you'll calculate that it moves "a positive distance". Here the important part comes, if the car is moving in the $+$ direction and the time the video is played is positive, i.e. I don't know if this will help, but it's the only way I can think of this in some intuitive sense. So in this case the $-2$ tells you to walk left a distance of $2$ miles but the $-3$ tells you to first turn around, and then walk $3$ times the $2$ miles in the other direction, so you'll end up walking right and end in the point that is $6$ miles to the right of the origin, so you'll be in the positive section, and $(-2)*(-3) = 6$.
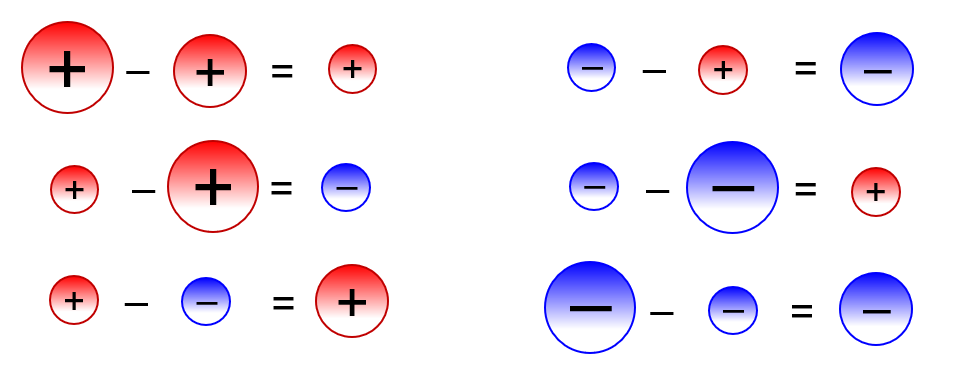
Maybe you could think of the negative sign in the second factor to imply that you change direction, that is, it makes you turn around and start walking the specified distance. Then how many times you will walk that distance? Just as before $3$ times and in the end you'll be $6$ miles to the left of the origin so you'll be in the negative section.įinally, you'll have to try to picture what could $(-2)*(-3)$ mean. With the same example in mind, what would $-2*3$ mean? First, suppose that the $-2$ just specifies that you will have to walk left a distance of $2$ miles. But in the same way you can play this idea with a negative times a positive. Now you picture where you're at? Well, you're at the right of the origin so you are in the positive section. Then I will try to convey the idea that if you are multiplying two numbers (let's suppose they are integers to make things easier to picture) then a product as $2*3$ would just mean that you have to walk right (in the positive direction) a distance of $2$ (say miles for instance) three times, that is, first you walk $2$ miles, then another $2$ miles and finally another $2$ miles to the right. If the signs are different, the answer is always negative.Įxample: -25 ÷ 5 = -5 Thus, these are the rules to add, subtract, multiply and divide positive and negative numbers.Well if I were to explain this in an intuitive way to someone (or at least try), I would like to think of an analogy with walking over the real line, by agreeing that walking left will be walking in the negative direction and walking right in the positive direction. If the signs are the same, the answer is always positive. (-) - (+) = Change the sign of the number to be subtracted and add them up.



 0 kommentar(er)
0 kommentar(er)
